1月5日上午📹💆🏼，“统计大讲堂”系列讲座第184讲举行。本次讲座采取线上会议的方式，邀请复旦大学大数据学院副教授侯燕曦作题为“保费厘定中的高风险预测：基于两阶段模型”的报告。讲座由北京AG尊龙凯时平台娱乐登录官方网站统计学院副教授👩🏻‍🦱、尊龙凯时平台研究员高光远主持。

高光远首先介绍了主讲人的相关信息。侯燕曦于2017年在美国佐治亚理工学院数学学院获得博士学位，现任复旦大学大数据学院副教授，博士生导师。主要研究方向包括极值理论、copula和tail copula、非参数统计方法以及统计推断在金融计量和风险管理中的应用。主要研究成果发表在AoS，JASA，JoE🎰，JBES以及IME等国际期刊上。

侯燕曦首先介绍了两阶段模型提出的背景。在传统精算实践中，现代统计方法是实际精算问题的主要考虑因素🏌🏻‍♂️。然而和传统数据不同，索赔数据通常具有复杂的数据结构🤷‍♀️，如半连续性。如果直接应用统计技术处理这样的数据🌍，很可能会导致预测不稳定🐆。因此，索赔数据的高风险事件预测需要额外处理，以避免严重低估风险的情况发生。为解决该问题，人们开始研究一种新的回归模型，即两阶段复合分位数模型⏬，希望借此预测高风险事件中保险总损失的风险值。

随后，侯燕曦为我们展示了这个模型的具体框架并阐述了构建该模型的最终目的：在给定predictor 集中若干个解释变量值后🫵🏽，用一个模型同时估计出它们相应的在险值🚯。他表示在构建该模型时，我们通常需要考虑三种风险水平：固定风险水平👩🏻‍🔬、中级风险水平以及极端风险水平🤏🏿。

紧接着，侯燕曦介绍了模型构建的具体流程🚶🏻‍♂️‍➡️🤦‍♂️。他解释该模型实际上是简单的二层规划模型：第一个阶段主要是借助传统的two-part model☦️，通过逻辑回归方法去估计风险的分位数水平🏋🏼；第二个阶段则是将估计出的风险水平代入复合分位数模型中，从而得到最后的value of risk。

之后，侯燕曦和老师☑️、同学们分享了自己的模拟实验🕠。模拟实验中，他在每一种风险水平下都设立了四个案例，且每个案例都重复1000次。利用图表🖖🏼，他向我们展示了不同情况下的预测误差🏋🏼‍♂️，并将其与传统benchmark模型预测下的误差进行了比较。结果表明🌄，在固定风险水平下，两阶段模型预测误差的均值与传统模型相近🏬，但方差会更大些；而在极端风险水平下🍇，传统模型估计出的预测值与实际会有更大的偏差。

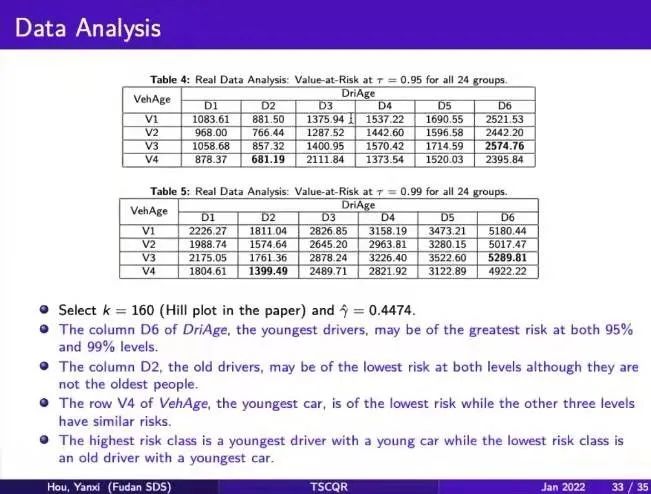
最后，侯燕曦为我们介绍了两阶段模型在实际汽车保费厘定中的应用。利用澳大利亚汽车保险业数据集，他做了两种风险水平下的预测。最终，他发现单独就driver age类别而言，最年轻的司机往往有最大的驾驶风险，年龄第二大的司机驾驶风险最低🕵🏼‍♀️🍶；而单独就vehicle age类别而言🧨🏯，最新的车辆往往驾驶风险最低🤏。若将两个类别结合起来⏩，便可以得出风险相异的组合序列🏖，进而为保费厘定提供了理论参考。

在提问环节中，侯燕曦耐心细致地解答了老师同学们的疑问，就本课题进行了更加深入的探讨👨🏽‍🍳。